In my review of Cross Blocks I said that to find the solution to the puzzles "some amount of trial and error is probably needed". I have to take that back somewhat, because after finding the right strategy I've become quite good at solving the puzzles on the first attempt.
This is a really good logic puzzle, so I'd like to share my findings.
SPOILER ALERT: don't read past this line if you want to find the strategies yourself.
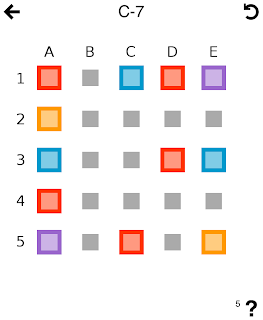
So let's take a look at the above puzzle, where I added coordinates along the edge to make it easier to explain.
The first thing we want to do in any Cross Blocks puzzle is count how many squares there are of each color. When there is an odd number of squares of one color, it means that three of them must be removed at the same time, which limits what we can do with them.
In the puzzle above there are:
3 blue
4 orange
5 red
5 violet
Since there are only 3 blue, there is only one way to remove them: tapping C3. Before being able to do that, we must remove a violet, an orange and a red square.
Let's look at the violets. There are 5, so we have to make one move to remove three of them. Such a move requires two of the squares to be on the same row or colum, so there are two options: E1+E4+C2 and C4+E4+C2.
E1+E4+C2 would require to remove a blue square first. But C2 is one of the squares that prevent that square to be removed, so this move is impossible.
We have to do C4+E4+C2 then, which requires removing two orange squares. It's easy to see that we cannot use the orange square in A2, because it's blocked by the violet in C2 and the blue in A3. Therefore the only way to remove the two orange squares is together, by tapping on C4.
Now we can remove the three violets by tapping on C4 again.
Let's look at the five red squares now. We again have two options for the three-piece move: A1+D1+C5, and A1+A4+D3. Both of them are blocked by a blue square, so we must get rid of the blues first. This is prevented by the red in D3, which implies that we must remove that piece with a two-piece move, so the three-piece move left is A1+D1+C5. The other red square left is A4, so the move we should do now is D3+A4, by tapping on D4.
We can finally remove the blue squares:
Then the red squares:
And now it's trivial to finish.
As I was writing this post, Google+ Auto Awesome thought it was so cool that it collated the images into an animated gif and sent it to me, so I guess I can paste it here :-)
©2013 Nicola Salmoria. Unauthorized use and/or duplication without express and written permission is strictly prohibited. Excerpts and links may be used, provided that full and clear credit is given to Nicola Salmoria and nontrivialgames.blogspot.com with appropriate and specific direction to the original content.